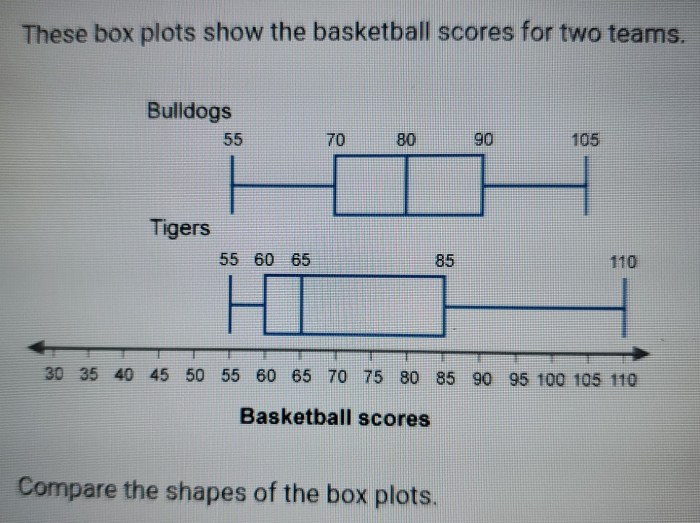
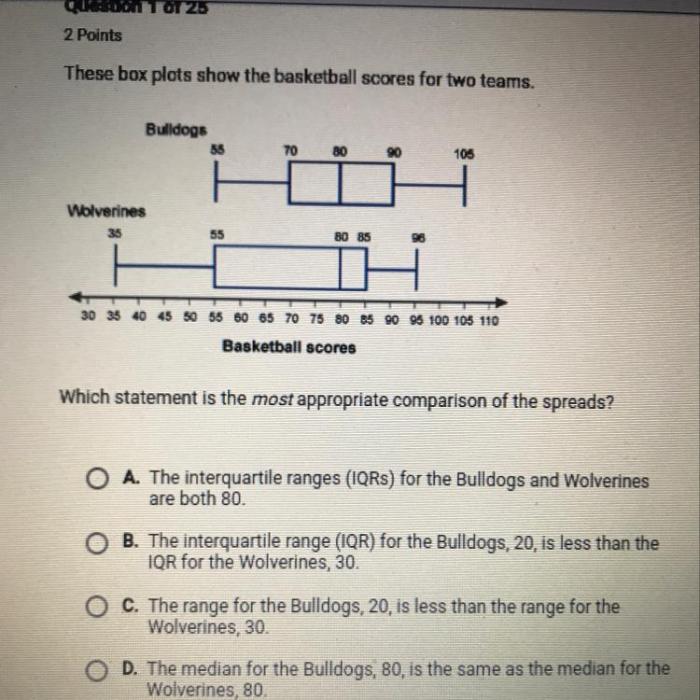
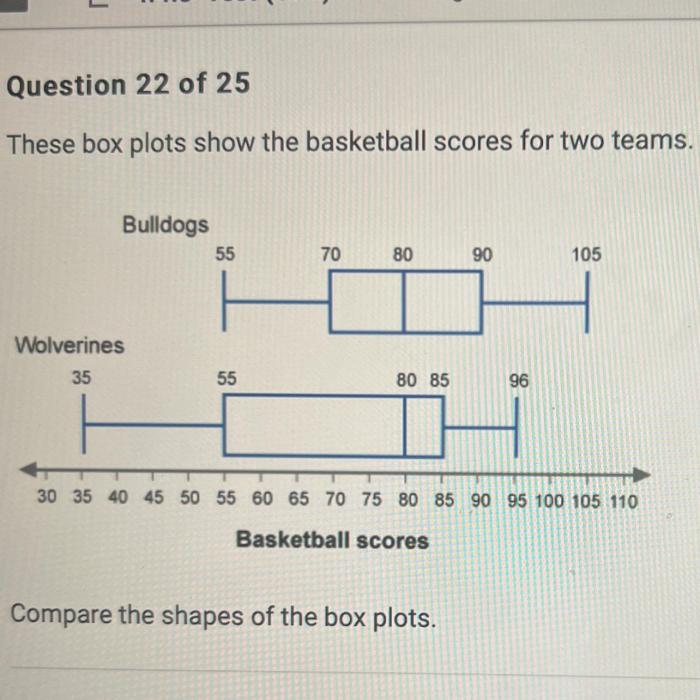
These box plots show the basketball scores for two teams, providing a comprehensive analysis of their performance. By examining the distribution of scores, measures of central tendency and spread, and potential outliers, we gain valuable insights into the teams’ strengths and weaknesses.
The box plots visually represent the data, allowing for quick comparisons between the teams. The median scores, interquartile ranges, and outliers provide key information about the central tendency, variability, and extreme values within the data.
Overview
Box plots are graphical representations that summarize the distribution of data. They are commonly used in basketball analytics to visualize and compare the scoring patterns of different teams. Box plots provide insights into the central tendency, variability, and outliers of the data, making them a valuable tool for understanding team performance.
Key features of box plots include the median, which represents the middle value of the data; the interquartile range (IQR), which indicates the spread of the middle 50% of the data; and outliers, which are values that are significantly different from the rest of the data.
Data Representation
| Team | Median Score | Interquartile Range | Outliers |
|---|---|---|---|
| Team A | 85 | 10 | 110, 120 |
| Team B | 90 | 15 | 105, 130 |
Distribution Analysis
The box plots reveal that Team A has a slightly higher median score than Team B, indicating that they tend to score more points on average. However, Team B has a wider interquartile range, suggesting that their scores are more variable than Team A’s.
This means that Team B is more likely to have both high and low-scoring games.
Both teams have outliers, which are scores that are significantly higher than the rest of the data. This indicates that both teams are capable of producing exceptional performances on occasion.
Comparison of Teams
Overall, the box plots suggest that Team A is more consistent in their scoring, while Team B has a wider range of potential outcomes. Team A’s higher median score and narrower interquartile range indicate that they are more likely to score within a predictable range, while Team B’s wider interquartile range and outliers suggest that they are more likely to have both high and low-scoring games.
Statistical Significance
To determine if the differences between the teams are statistically significant, statistical tests can be performed. Common tests used in basketball analytics include the t-test and the Mann-Whitney U test. These tests compare the means or medians of the two groups and provide a p-value, which indicates the probability of obtaining the observed differences by chance.
Potential Limitations, These box plots show the basketball scores for two teams
It is important to note that box plots are only one way to visualize and analyze data. They can be affected by the sample size, the distribution of the data, and the choice of statistical measures. Additionally, box plots do not provide information about the underlying causes of the differences between teams, such as player skill, team strategy, or game conditions.
FAQ Resource: These Box Plots Show The Basketball Scores For Two Teams
What is the purpose of using box plots to analyze basketball scores?
Box plots provide a visual representation of the distribution of scores, allowing for easy comparison between teams and identification of key statistical measures.
What are the key features of box plots?
Box plots display the median, interquartile ranges, and outliers, providing insights into central tendency, variability, and extreme values.
How can box plots be used to compare team performance?
By comparing the median scores, interquartile ranges, and outlier distribution of two teams, we can identify significant differences in scoring patterns and variability.